Understand Bubble Sort Algorithm

Bubble Sort is a simple sorting algorithm that repeatedly steps through the list, compares adjacent elements, and swaps them if they are in the wrong order. This process continues until the list is sorted.

Understanding the Algorithm

1. Iterate through the list: Start from the first element and compare it with the next one.
2. Compare and swap: If the current element is greater than the next one, swap them.
3. Repeat: Move to the next element and repeat steps 1 and 2 until you reach the end of the list.
4. Outer loop: After one pass, the largest element will be at the end of the list. Repeat the entire process (outer loop) until the list is sorted.

Ruby Implementation

Here’s a Ruby implementation of Bubble Sort:

def bubble_sort(array_to_sort)
  array_length = array_to_sort.length

  (1..array_length - 1).each do
    (1..array_length - 1).each.with_index do |i, _index|
      first_element = array_to_sort[i - 1]
      second_element = array_to_sort[i]

      if array_to_sort[i - 1] > array_to_sort[i]
        array_to_sort[i] = first_element
        array_to_sort[i - 1] = second_element
      end
    end
  end
  # Return the sorted array
  array_to_sort
end

# Example usage
unsorted_array = [64, 34, 25, 12, 22, 11, 90]
sorted_array = bubble_sort(unsorted_array)
puts sorted_array

You could see this example going to this repository

Explanation:

• Outer loop: Iterates array_length - 1 times, where array_length is the length of the array.
• Inner loop: Iterates from each element in thea array in each outer loop iteration.
• Comparison and swap: Compares adjacent elements and swaps them if they are in the wrong order.
• Early termination: If no swaps occur in an outer loop iteration, the list is already sorted, and the algorithm can terminate early.

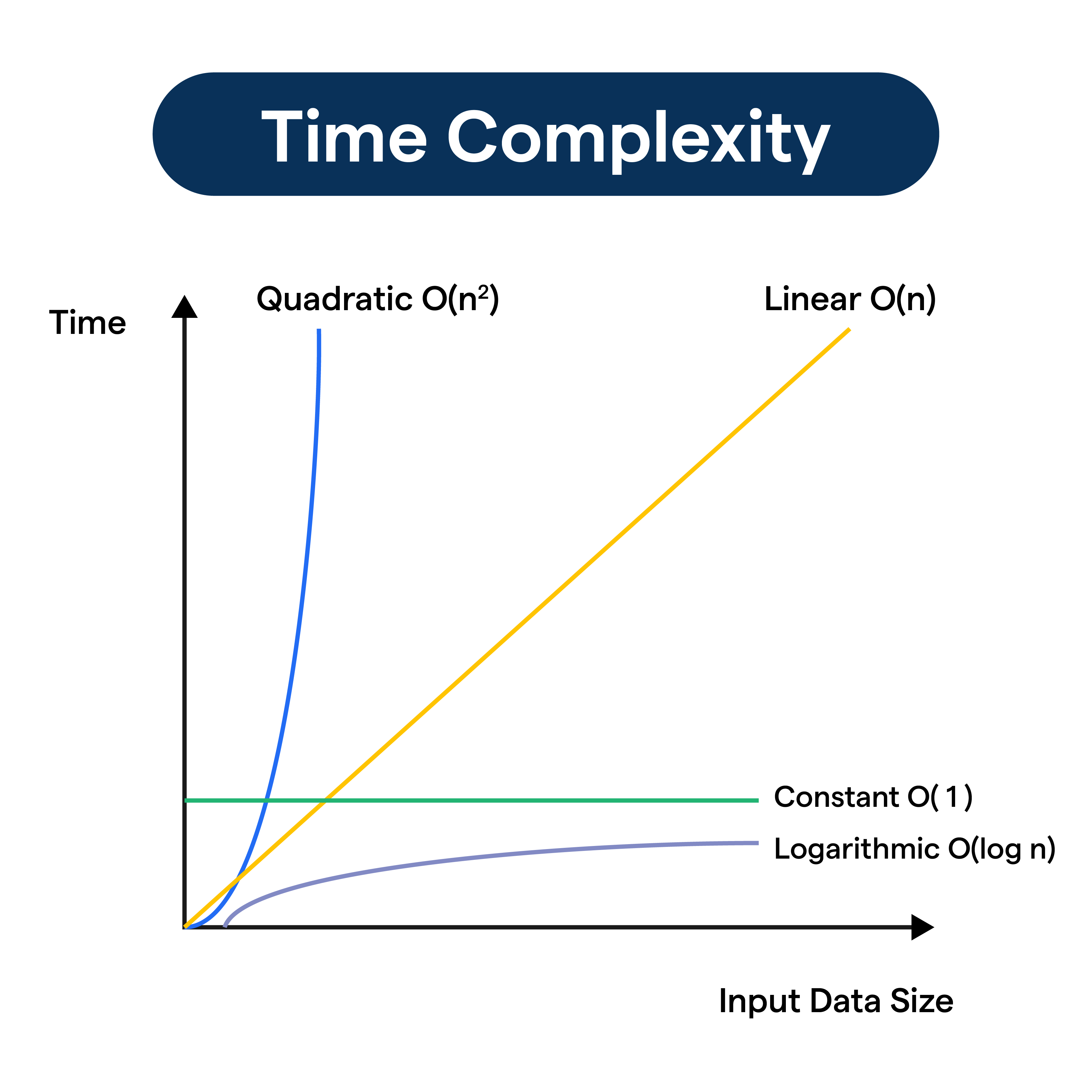
Time Complexity

Bubble Sort has a time complexity of O(n^2) in the worst-case scenario, which occurs when the array is already sorted in reverse order. In the best-case scenario (array is already sorted), the time complexity is O(n).

Conclusion

Bubble Sort is a simple but inefficient sorting algorithm. While it’s easy to understand and implement, it’s not suitable for large datasets due to its quadratic time complexity. For more efficient sorting, consider algorithms like Merge Sort, Quick Sort, or Heap Sort.